%%HTML
<!--
<style>
.container {width:70% !important;}
</style>-->
%matplotlib inline
from __future__ import division
import kwant
from matplotlib import pyplot
import matplotlib
import numpy as np
import scipy.linalg
import scipy.sparse.linalg
import kwant.graph.dissection
import tinyarray as ta
import math
from matplotlib.patches import Circle
from math import sqrt
from cmath import exp
subplot = pyplot.subplot
matplotlib.rcParams['figure.dpi'] = 320
matplotlib.rcParams['figure.figsize'] = (10, 5)
sys = kwant.Builder()
lat = kwant.lattice.square()
sys[lat.shape((lambda pos: pos[0]**2 + pos[1]**2 < 8**2), (0,0))] = 10
sys[lat.neighbors()] = 1
sys = sys.finalized()
h = sys.hamiltonian_submatrix().real
reordering = np.r_[tuple(kwant.graph.slice(sys.graph, 0, 1))]
h_rgf = h[reordering][:, reordering]
dis = kwant.graph.dissection.edge_dissection(sys.graph, 1)
def flatten(a):
x, y = a
if isinstance(x, tuple):
x = flatten(x)
if isinstance(y, tuple):
y = flatten(y)
return x + y
dis = flatten(dis)
h_diss = h[dis][:, dis]
#Generate the system plot
def circle(pos):
x, y = pos
return x**2 + y**2 < 20
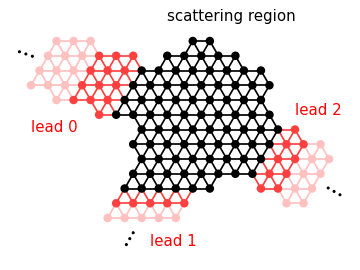
lat = kwant.lattice.triangular()
sys = kwant.Builder()
sys[lat.shape(circle, (0, 0))] = 0
sys[lat.neighbors()] = 1
lead_dirs = [lat.vec((-3, 1)), lat.vec((0, -1)), lat.vec((2, -1))]
for d in lead_dirs:
lead = kwant.Builder(kwant.TranslationalSymmetry(d))
lead[lat.wire((0, 0), 2.1)] = 0
lead[lat.neighbors()] = 1
sys.attach_lead(lead)
fig = kwant.plot(sys, show=False)
ax = pyplot.gca()
pyplot.text(-2, 5.5, 'scattering region', size=15)
pyplot.text(-10, -1, 'lead 0', color='red', size=15)
pyplot.text(-3, -7.7, 'lead 1', color='red', size=15)
pyplot.text(5.5, 0, 'lead 2', color='red', size=15)
for dir, offset in zip(lead_dirs, [10.5, 8, 8.6]):
dir = np.array(dir) / math.sqrt(np.dot(dir, dir))
for i in [0, 0.4, 0.8]:
ax.add_artist(Circle(dir * (offset + i), 0.06, fc='k'))
pyplot.axis('off')
pyplot.xlim((-11, 9))
pyplot.ylim((-8, 6))
fig.tight_layout()
fig.set_size_inches(*(5, 3.75))
fig.savefig("tbsys.png")

Numerical simulation of quantum transport¶
Christoph Groth, Michael Wimmer, Anton Akhmerov, and Xavier Waintal
I will tell¶
- What is a scattering problem.
- What algorithms exist to solve it.
How to use Kwant to define and solve such problems (here we run some code).
- If you want to run code and don't have Kwant yet, get an account at http://cloud.sagemath.com/ now.
- Also please fill out the Kwant user survey at
http://kwant-project.org/2015-survey
The tight-binding scattering problem¶
Now to get conductance and other observables,
we only need to calculate $\Sigma_{\textrm{lead}}$, $G^R$, $G^<$, and we're done.
(that is what one mostly hears)
But there is a more intuitive definition.
The tight-binding scattering problem¶

has the Hamiltonian:
$$ H = \begin{pmatrix} \ddots & V_L\\ V_L^\dagger & H_{L}& V_{L}\\ & V_{L}^\dagger & H_L & V_L\\ & & V_L^\dagger &H_S\\ \end{pmatrix}, \quad \psi = \begin{pmatrix} \vdots \\ \psi_2 \\ \psi_1 \\ \psi_S \end{pmatrix} $$($H_L$ and $V_L$ are block-diagonal if there are many leads)
Modes in the leads¶
Since the leads are translationally invariant,
the lead wave function can be decomposed into eigenvectors of translation (lead modes)
the modes in the leads satisfy
$$ V_L \psi_0 + H \lambda \psi_0 + V_L^\dagger \lambda^2 \psi_0 = 0, $$or in a matrix form:
$$ \begin{pmatrix} -V_L^{-1} H_L & -V_L^{-1} \\ V_L^\dagger & 0 \end{pmatrix} \begin{pmatrix} \psi_0 \\ V_L^\dagger \psi_1 \end{pmatrix} = \lambda^{-1} \begin{pmatrix} \psi_0 \\ V_L^\dagger \psi_1 \end{pmatrix} $$...or in a more stable form (and reduced basis):
$ \tilde{H} = H_L + i AA^\dagger + i BB^\dagger,\quad V_L = A B^\dagger, \quad \tilde{\psi}_0 = B^+ \psi_0, \quad \tilde{\psi}_1 = A^+ \psi_1 $
Incoming and outgoing modes¶
Split all the eigenvectors into incoming, outgoing and evanecsent, such that:
$$\langle\psi_{\textrm{in}}|\hat{I}|\psi_{\textrm{in}}\rangle = 1$$$$\langle\psi_{\textrm{out}}|\hat{I}|\psi_{\textrm{out}}\rangle = -1$$$$\langle\psi_{\textrm{evan}}|\hat{I}|\psi_{\textrm{out}}\rangle = 0, \quad |\lambda_{\textrm{evan}}| < 1$$Finally, the equations to solve¶
Substituting the lead modes into Hamiltonian gives a linear system:
$$ \begin{split} \begin{pmatrix} - U_{\text{out}} & 1 \\ V_{L}^\dagger U_{\text{out}}\Lambda_{\text{out}} & H_\text{S} \end{pmatrix} \begin{pmatrix} \mathbf{S}\\ \psi_S \end{pmatrix} = \begin{pmatrix} U_{\text{in}}\\ -V_{\text{L}}^\dagger U_{\text{in}} \Lambda_{\text{in}} \end{pmatrix} \end{split}, $$with $U_{\text{in}}$ and $U_{\text{out}}$ wave functions of incoming and outgoing modes, and $\Lambda\equiv \textrm{diag}(\lambda_i)$.
From now on, we only need to write down these linear equations and solve them.
(NB: if we start by eliminating $\mathbf{S}$, the rhs becomes $H_S + \Sigma$)
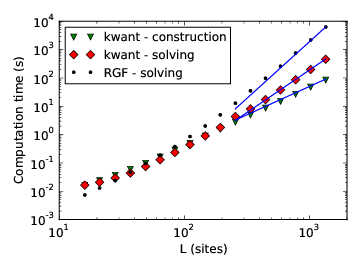
Solving a linear system¶
Take a tight-binding system, assign #'s to sites, write down the matrix
kwant.plot(sys, ax=subplot(121, aspect='equal'), show=False)
h = sys.hamiltonian_submatrix().real
pyplot.spy(h, axes=subplot(122));
Naive solution¶
Perform gaussian elimination beginning to end:
pyplot.spy(h, axes=subplot(1, 2, 1))
p, l, u = scipy.linalg.lu(h)
pyplot.spy(l + u, axes=subplot(1, 2, 2));
Better idea (what most physicists would do)¶
Rearrange the sites into slices
(also known as recursive Green's functions)
pyplot.spy(h_rgf, axes=subplot(1, 2, 1))
p, l, u = scipy.linalg.lu(h_rgf)
pyplot.spy(l + u, axes=subplot(1, 2, 2));
What sparse linear algebra packages do¶
A hierarchic rearrangement (nested dissection)
pyplot.spy(h_diss, axes=subplot(1, 2, 1))
p, l, u = scipy.linalg.lu(h_diss)
pyplot.spy(l + u, axes=subplot(1, 2, 2));
Algorithm of how to solve the scattering problem¶
- Construct a linear system of equations
(the one with lead modes) - Solve it efficiently
(so use a sparse linear algebra library)
Now let us solve some problems :-)
If you do not know python yet, you are missing a lot of fun.
Defining tight-binding systems (in kwant)¶
- There are many different tight binding systems
- There are only few sparse linear algebra libraries
- Libraries know of graphs, systems know of lattices, spins, superconductors, and many more.
So let's separate defining the system:
kwant.Builder
from solving it:
kwant.SystemAn example¶
Quantum Hall effect in a graphene with a quantum point contact
- Import the required packages
%matplotlib inline
from matplotlib import pyplot
import kwant
- Create the system and a lattice
hallbar = kwant.Builder()
graphene = kwant.lattice.general([[1, 0], [1/2, sqrt(3)/2]], # Unit vectors
[[0, 0], [0, 1/sqrt(3)]]) # Site positions
- Define the shape of the scattering region
def scattering_region(pos):
x, y = pos
return -50 < x < 50 and -30 < y < 30 and y**2 - x**2 < 14**2
hallbar[graphene.shape(scattering_region, (0, 0))] = 0.
Example (continued)¶
- Define the value of the hoppings (it depends on magnetic field and coordinates)
- Add the hoppings to the system
- Remove dangling bonds
def hopping(site1, site2, B=0.01):
x1, y1 = site1.pos
x2, y2 = site2.pos
return -1 * exp(1j * B * (x1 - x2) * (y1 + y2))
hallbar[graphene.neighbors(1)] = hopping
# graphene.neighbors(2) for next-nearest neighbors
hallbar.eradicate_dangling()
Example (continued further)¶
- Repeat the same for the leads.
Leads are similar, only they have a translational symmetry
lead = kwant.Builder(kwant.TranslationalSymmetry((1, 0)))
def lead_shape(pos):
return -30 < pos[1] < 30
lead[graphene.shape(lead_shape, (0, 0))] = 0.
lead[graphene.neighbors()] = hopping
- Attach the leads
hallbar.attach_lead(lead)
hallbar.attach_lead(lead.reversed());
Example (ready to solve)¶
- Check the result
kwant.plot(hallbar, site_size=1);
- Finalize the system
hallbar = hallbar.finalized()
Example (finally)¶
- Solve linear systems!
muvals = np.linspace(0.1, 0.4, 200)
conductances = [kwant.smatrix(hallbar, energy=mu).transmission(0, 1)
for mu in muvals]
pyplot.plot(muvals, conductances);
Example: solve more¶
- calculate local density of states
ldos = kwant.solvers.default.ldos(hallbar, 0.20, args=[0.01])
kwant.plotter.map(hallbar, ldos, colorbar=False, cmap='gist_heat_r');
Exact diagonalization¶
- Find 6 eigenstates closest to Fermi level
h = hallbar.hamiltonian_submatrix(sparse=True).tocsc()
scipy.sparse.linalg.eigsh(h, sigma=0.1)[0]
array([ 0.09658392, 0.10469133, 0.08859576, 0.1129415 , 0.08079808,
0.12134041])
Conclusions¶
- Quantum transport is as easy as defining and solving linear systems of equations.
- Defining tight such systems can be made easy.
- Solving them is also easy if using good libraries and clever algorithms.
Check Kwant out at http://kwant-project.org
More code examples:¶
- Basic stuff: http://downloads.kwant-project.org/examples/
- Topological stuff: http://topocondmat.org
- My favorite: http://arxiv.org/abs/1408.1563 (see ancillary files)
- For a reference:
Examples from research¶
Statistical topological insulators (arXiv:1212.6191)¶
- Like topological insulators, but protected also in presence of disorder that breaks the symmetry
- A quasi-1D $p_x$-wave superconductor has edge transmission $T\sim L^{-1/2}$, since the edges form disordered Majorana chains at the critical point
- Doubling the number of sites per unit cell localizes the system
Statistical topological insulators (arXiv:1212.6191)¶
- Any translationally invariant lattice with 1 Majorana fermion per unit cell becomes metallic $T\sim \log(L)$ after adding disorder.
Soft gap in Majorana wires (in preparation)¶
- What role does geometry of the nanowire experiment play?

- Different transverse modes in the wire have different flight times.
- Induced gap is inversely proportional to the flight time
- In ballistic samples the induced superconducting gap becomes soft: $\rho(E) \sim |E|$, for $|E| < \Delta_{\textrm{max}}$

- Disorder kills the trajectories with longest flight time first.
- There is a large range of disorder strengths, where the gap is soft and Majorana fermions are present

Thank you all.
The end.
out = !ipython nbconvert kwant_presentation.ipynb --to slides